Hydrologic Model Calibration in the National Weather Service
Michael B. Smith1, Donald P. Laurine2, Victor I. Koren1, Seann M. Reed1, and Ziya Zhang1
ABSTRACT
Comprehensive procedures have been developed by the NWS for calibration of the conceptual
hydrologic models used in river forecasting. These procedures are designed to achieve model parameters
that are consistent between calibration and operational forecasting. Using these procedures, model
parameters are derived using calibration data sets in a way that minimizes biases and errors when used in
operational forecasting using real time estimates of precipitation, temperature, and evaporation. An
overview of the data analysis techniques and manual calibration steps for rainfall-runoff models is
presented. Future enhancements to the calibration process will also be discussed.
1. INTRODUCTION
The National Weather Service (NWS) has a mandate to provide forecasts for the Nation's rivers. To fulfill this mission,
the NWS uses its River Forecast System (NWSRFS) at 13 River Forecast Centers (RFCs) to provide daily stage forecasts
at over 4,000 points. Research and development to support the NWSRFS is conducted within the Hydrology Lab (HL)
of the NWS Office of Hydrologic Development (OHD). Within the NWSRFS are algorithms for hydrologic and
hydraulic models as well as procedures for data ingest, display and analysis of results, and other functions. Interested
readers are referred to Stallings and Wenzel [1995], Larson et al., [1995], Fread et al., [1995], and Monroe and Anderson
[1974] for more information regarding the structure and mission of the NWS river forecasting program.
While calibration of hydrologic models is widely considered a standard step in any application, the mandate assigned
to the NWS to forecast the Nation's rivers has immense implications regarding the calibration and implementation of
hydrologic and hydraulic models on a national scale. Since the introduction of calibration procedures over two decades
ago, [Brazil and Hudlow, 1981], a great deal of effort has been directed toward improving and streamlining the
calibration procedures. The purpose of this paper is to present an overall view of the current NWS hydrologic model
calibration process, from deriving the input data sets to incorporating the calibrated parameters and other information
into the operational forecasting system. Contained within the NWSRFS are also hydrologic and hydraulic channel
routing algorithms. However, the calibration of these models is beyond the scope of this paper.
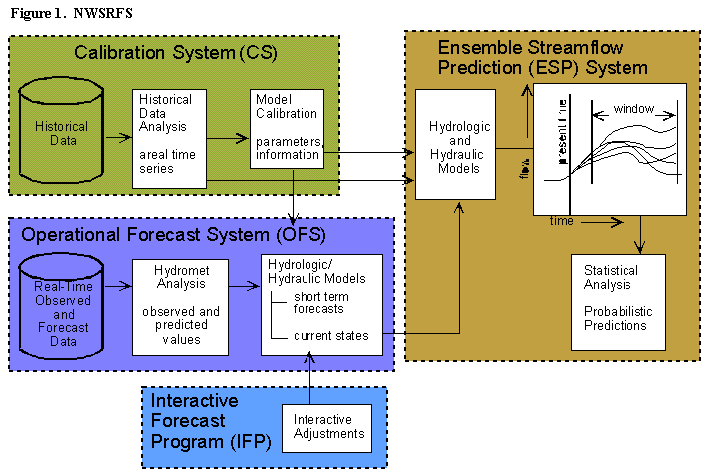
Figure 1 presents the major components of the NWSRFS and shows that the Calibration System (CS) is a significant
component of the entire functional structure. In the CS, time series of historical forcings are prepared and model
parameters are calibrated. In the Operational Forecast System (OFS), real time data are used with the calibrated
hydrologic and hydraulic models to produce forecast river stages several days into the future. The Interactive Forecast
Program (IFP) allows the hydrologist to make run-time adjustments to account for non-standard conditions. The historical
time series of precipitation, temperature, and potential evaporation are used to generate a suite of long term probabilisitic
forecasts weeks or months into the future in the Ensemble Streamflow Prediction system (ESP). Statistical procedures
are used to quantify the uncertainty of these forecasts within a designated window.
The primary rainfall-runoff model used for operational forecasting in the NWS is the Sacramento Soil Moisture
Accounting (SAC-SMA) model. Methods described in this paper will address the calibration of the parameters of the
SAC-SMA. Interested readers are referred to Koren et al., [this volume], Burnash et al, [1973], Burnash [1995] and
Finnerty et al., [1997] for more complete descriptions and applications of the SAC-SMA model.
Basically, the SAC-SMA is a two layer conceptual model of a soil column, with several modifications to account for the
spatial variability of certain processes. Six types of runoff can be generated to form a complete runoff hydrograph. Each
of the two layers in the SAC-SMA contains a tension water and free water component. Rain falling on the soil column
first encounters the upper zone. Here, rain falling on any impervious areas generates impervious area runoff, while rain
falling on the non-impervious areas of the basin first encounters the upper tension water storage. After filling this
reservoir, excess soil water enters the upper zone free water. Water in this free water storage can percolate into the lower
zone storages or flow out as interflow. If the upper zone free water fills completely, then excess soil water flows out as
surface runoff. Most percolated water flows into the lower zone tension water storage, although some can go directly
to free water storages in the lower zone. Upon filling the lower zone tension water storage, all soil water moves into the
two lower zone free water storages. These two free water storages generate fast and slow responding base flow. The
combination of these two base flows is designed to model a variety of hydrograph recessions. The SAC-SMA also has
a variably-saturated area component from which saturation excess runoff is generated.
The snow model within NWSRFS is the snow accumulation and ablation model (Snow-17) developed by Anderson
[1973]. Snow-17 is a conceptual model of a point snow column with an areal depletion curve used to determine the
portion of the area being modeled that has snow cover. Snow-17 uses temperature as an index for the amount of energy
exchange at the snow-air interface with separate equations for rain-on-snow and non-rain melt and for heat transfer during
periods when melt is not occurring. The major Snow-17 parameters that are calibrated include those that control the
seasonal variation of non-rain melt events, and areal depletion curve parameters. Overall results from Snow-17 compare
favorably to those obtained with a complete energy balance model except during unusual meteorological situations such
as periods with high dew-points and wind speeds [Anderson, 1976]. Further research is underway in HL to compare
Snow-17 with energy balance models.
2. THE VALUE OF CALIBRATION IN THE NWS
Model calibration leads to obvious major benefits for operational forecasting. With a well calibrated model, real time
simulations should more closely follow observed streamflow, resulting in more accurate forecasts with a longer lead-time
into the future. Such well-calibrated models should require fewer run-time modifications to keep the models on track.
Also, models that can simulate historical conditions with a known degree of accuracy allow for reliable probabilistic
forecasts to be made for predictions of streamflow and other variables weeks or months into the future.
In addition, the manual calibration process also allows the user to develop a much deeper understanding of the data and
the models and their limitations. This process is a chance for the calibrator to develop an understanding of the sensitivity
of model parameters, interactions between parameters, effects of hydrologic inputs, and the knowledge of system
mechanics. Calibration is an important evolutionary step in the development of an effective hydrologic forecaster who
will be better able to apply the models for operational use.
Operationally, the forecaster is often required to make many adjustments to the hydrologic model to account for model
and data errors. These adjustments are critical to the ability of the system to properly forecast future events. There are
many options available for the forecaster to accomplish the same result in simulating the forecast hydrograph. Through
guided interactive trail and error calibration, the hydrologist gains knowledge and experience to be used in selecting the
proper adjustment.
Another important value gained through calibration is an understanding of the physical process occurring in the
watershed and how well the calibrated model simulates those processes. Most river basins are very complex. For
example, a typical basin in the western U.S. can be affected by reservoir operations; diversions, agricultural consumptive
use, return flows, and basin geographical variability. Many of the current hydrologic models can only approximate these
physical processes. Through calibration, the forecaster can build an awareness of model limitations and basin processes.
The information gained provides the level of confidence the forecaster places on the forecast procedure.
Two basic approaches exist for the calibration of model parameters. The first is a manual trial-and-error method
[Anderson, 2002], and the second involves the use of automated optimization programs. For the conceptual models
currently in use in the NWS, interactive manual calibration that follows a logical strategy is recommended in order to
preserve the physical basis of the model parameters and an appropriate variability of the parameters among watersheds
in a basin. Automatic optimization can be used in conjunction with the manual steps. At various points in the calibration
process, many tools including geographic information system (GIS) based programs are available to assist the
hydrologist.
3. REGIONAL APPROACH FOR CALIBRATING A RIVER BASIN
It is usually recommended that data analysis and calibrations be performed on a large area or river basin basis rather than
on an individual watershed for several reasons. Details of this procedure can be found in publications by Anderson
[2002] and a comprehensive calibration training video developed by the NWS in conjunction with the Hydrologic
Research Center [Hydrologic Research Center, 1999]. First, the meteorologic processes that control the development
of precipitation, temperature, and evaporation variations occur on a scale much larger than a typical watershed, especially
in mountainous areas. In order to properly understand these processes, the data analysis should be performed on a
regional and not watershed scale. Such an approach also facilitates more efficient historical data retrieval and analysis
since many precipitation, temperature, and other stations are common to several watersheds in a basin. If historical data
analysis is performed on a watershed by watershed basis, then redundant downloading and processing of station data
occurs.
Second, it is much more likely to achieve a realistic and consistent set of parameters using a strategy that examines the
spatial variability of physiographic features and hydrograph response to guide the variation of parameters among
watersheds within a basin. Physiographic features which affect model parameters such as topography, type of soils, and
vegetation can be viewed to note areas of significant similarity or difference. Such qualitative information can be used
to subjectively determine how model parameters can be expected to vary across a basin. If such physiographic features
appear to be spatially invariant, the analyst can expect that the calibrated parameters from one watershed can be used
as reasonable starting points for calibration of a neighboring watershed, resulting in a more efficient calibration effort.
Observed streamflow data show the integrated effects of all basin features and can also be used to qualitatively assess
the spatial variability of hydrologic model parameters across watersheds in a basin. Observed discharges can be scaled
to the drainage area of one of the watersheds and then plotted on semi-log scale. Hydrographs that show similarities in
base flows and storm runoff indicate that the hydrologic model parameters could be quite similar to one another.
4. SOURCES OF DATA FOR MODEL CALIBRATION
The primary source of historical data for model calibration is the National Climatic Data Center (NCDC), which collects
and maintains an archive of measurements of precipitation, temperature, evaporation, and other meteorologic variables.
Data in digital form is readily available starting in 1948, with recent efforts underway to convert the entire period to
digital format. In HL, recent work has begun to develop direct Internet links to the NCDC archive through web servers
[G. Bonnin, NWS HL, personal communication, 2001]. Such efforts should alleviate the need for the NWS to maintain
its own archive of the NCDC data sets.
Streamflow data have traditionally been available from the United States Geological Survey (USGS) in the form of mean
daily flow. For many years, these were the only observed streamflow data available for hydrologic model calibration
in the NWS. Mean daily flow data are derived from hourly or sub-hourly streamflow measurements (unit values) that
have been quality controlled. Recently, the USGS has been making available unit value streamflow data from its local
field offices for research and calibration needs. These data are provisional in that no quality control procedures have
been performed on them. Calibration at sub-daily time steps is critical as the NWS moves to hydrologic modeling at finer
spatial and temporal time scales as part of its distributed modeling efforts for river and flash flood forecasting [Zhang
et al., 2001; Smith et al., 1999]. Other data available from the USGS are limited peak flow data, as well as reservoir
pool elevation data.
An emerging source of data for model calibration is the archive of operational real time data collected each day at the
13 RFCs. As part of their operations, RFCs can receive thousands of observations of temperature, precipitation, and
streamflow each day. These data are stored in custom data bases within NWSRFS and are processed to generate daily
river forecasts. On a regular basis, a copy is made of these data and stored in the NOAA Hydrologic Data System
(NHDS) to become available for future calibration efforts and research studies [Pan et al., 1998; Bonnin, 1996]. Data
from the NWS series of WSR-88D Next Generation Radar platforms (NEXRAD) are also included in the NHDS archive.
Individual RFCs often maintain their own archive of their operational data files. A limited set of utilities are available
for converting these data from an operational format to a standard format used in the calibration system. Currently,
efforts are underway to develop a consistent RFC archive data base design [D. Page, NWS HL, personal communication,
2002].
Other sources of data used for calibration include the Natural Resources Conservation Service (NRCS) and its Snowpack
Telemetry (SNOTEL) system. SNOTEL provides year round temperature and precipitation data in remote, mountainous
areas primarily in the western United States.
5. MAJOR STEPS IN THE CALIBRATION PROCESS
The calibration process is comprised of the following three general steps:
1. Analysis of historical data and derivation of time series of observed precipitation, temperature, and potential
evapotranspiration.
2. Calibration of hydrologic model parameters so that simulated streamflow agrees with observed data.
3. Implementing the calibrated parameters and data analysis information into the operational forecast system.
This step will not be explicitly discussed here. The interested reader is referred to Anderson [2002]
for details on this important issue.
5.1 Analysis of Historical Data
5.1.1. Overview. Analysis of historical data to derive multi-year time series of mean areal precipitation,
temperature, and potential evaporation proceeds according to the steps shown in Figure 2. Time series of precipitation
are derived using the Mean Areal Precipitation preprocessor (MAP) while corresponding mean areal time series of
temperature and potential evaporation are produced using the MAT and MAPE preprocessors, respectively. These time
series are then used as forcings in the calibration of hydrologic model parameters. Henceforth, the acronyms MAP, MAT,
and MAPE will denote both the times series of data as well as the preprocessor that computes them.
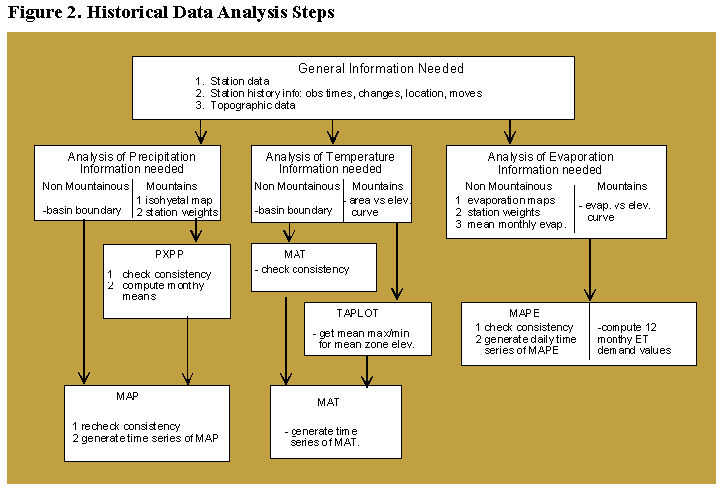
As shown in Figure 2, different analysis procedures are available for each variable depending on whether the area is non-mountainous or mountainous. For precipitation, an area is non-mountainous if the long term annual or seasonal station
means are within a range of ±5%. If the range is greater than this, the mountainous area analysis should be used.
Similarly, this criteria applies to the analysis of temperature and evaporation as well. In non-mountainous areas, it is
assumed that any station can be used to estimate missing data at another station without making any adjustments for
differences in magnitude. Moreover, spatial averages of the variables can be computed using station weights that are
based solely on their location in the x,y plane. In non-mountainous areas, the station weights always sum to a value of
1.0.
Terrain differences are usually the main factors requiring the use of mountainous area procedures for analyzing
precipitation, temperature, and evaporation. In these procedures, long term station means are accounted for in the
estimation of missing data and information other than simple station location is used to derive station weights for the
computation of areal averages. Station weights in mountainous areas usually sum to a value greater than 1.0. In
mountainous areas, watersheds are frequently sub-divided in order to properly model the accumulation and ablation of
the snow cover.
The HL-developed Calibration Assistance Program (CAP) contains data sets and tools that are primarily used for the
analysis of mountainous areas. CAP is a national ArcView GIS- based suite of tools that facilitates the derivation of
basin sub-divisions, model parameters, potential evaporation estimates, and mean areal estimates of precipitation and
temperature. Moreover, CAP also contains satellite snow cover maps that can be used in conjunction with observed
streamflow hydrographs and area elevation curves to identify different regimes that occur over the watershed. CAP also
contains vegetation maps to help identify such regimes. The Appendix provides more details about the functions available
in CAP.
It is very important that the resultant time series of precipitation, temperature, and evaporation are properly scaled to
accurately represent what actually occurred in nature. Tests have shown that 10% variations in MAP time series can
result in variations in simulated streamflow volumes of nearly 25% [Anderson, 2002]. Similar results have been reported
for biases in the MAT time series. Even a bias of a few degrees can cause a significant shift in the timing of snowmelt.
Parameters calibrated using such biased forcings will be distorted and lead to sub-optimal forecasts. Also, the MAP,
MAT, and MAPE time series derived in calibration are used for ensemble forecasting, so biases in these time series can
lead to degraded ensemble forecasts.
5.1.2. Station selection. Analysis begins with the selection of stations to be used to derive the historical time
series of mean areal precipitation, temperature, and in some cases evaporation. For precipitation, it is advisable to look
for hourly and daily stations with at least 5 and preferably 10 or more years of complete data. Since precipitation can
be quite spatially variable, all stations located in the basin having good quality data are selected, as well as some outside
the basin. For each daily station, it is important to note the location of hourly stations so as to have information needed
to disaggregate the daily values. In mountainous areas, stations further out from the basin may need to be used to
adequately represent higher elevations. In the current NWSRFS, only daily max/min temperature observations are used
to generate historical MAT time series. Given that temperature is generally less spatially variable than precipitation,
fewer temperature stations are required. Generally, all stations within and near the basin with long records are selected
for analysis. Additional stations outside the basin with shorter periods of record are used if needed to properly represent
high elevations. In contrast to precipitation stations, temperature stations with a long period of record are needed due
to limitation in the current processing programs. Pan evaporation sites and stations with meteorological data to compute
potential evaporation are selected to properly represent the variation in evaporation over the basin.
5.1.3. Quality control. Quality control procedures are applied to the station data prior to the derivation of time
series of mean areal values of the variables. These procedures are necessary to avoid having a bias between one period
of the calibration record and another. If an individual station receives considerable weight in the computation of the
mean areal value, then inconsistencies in the station data will be translated to the mean areal value time series.
Parameters calibrated from a period before the inconsistency will not be the same as parameters calibrated using the
period after the inconsistency. If the period used for calibration does not reflect the current status of the station, then
operational results will be biased.
The main quality control procedure for precipitation, temperature and potential evaporation data is to check the
consistency of a station using double mass analysis. Double mass analysis can be performed in the MAP, MAT, and
MAPE programs. Inconsistences appear as long term shifts in the general slope of the station accumulation curve. Such
inconsistencies can result from man-made changes in station location, changes in equipment (e.g., addition of a shield
to a rain gage), or changes in station exposure due to surrounding vegetation. Shifts due to such changes should generally
be corrected. Thus, station history information is critical to identifying man-made effects that must be corrected. Double
mass plots are displayed of stations grouped geographically, so that any shifts in one station can be compared to nearby
stations. Such grouping helps identify when natural climatic changes occur in a region. Shifts such as these should not
be corrected. Sharp discontinuities in double mass plots often indicate bad raw data values. In general, if there is any
doubt as to whether a consistency correction is necessary, it is advisable not to make the correction. Pan et al., [1998]
have developed the Interactive Double Mass Analysis (IDMA) tool, which is a graphical user interface to automate the
generation of double mass plots and correction factors.
5.1.4 Generation of mean areal precipitation time series. As seen in Figure 2, non-mountainous and
mountainous area procedures can be used to derive time series of mean areal values of precipitation. In non-mountainous
areas, any station can be used to estimate missing data at other stations. Also, simple station weighting schemes such as
Thiessen polygons or inverse distance squared weighting can be used to compute time series of mean areal precipitation
values using the MAP program.
For analysis of precipitation in mountainous areas, additional steps are needed that require the use of the Preliminary
Precipitation Processing Program (PXPP). The primary function of PXPP is to relate precipitation stations having
different periods of record by generating monthly means of all stations. These monthly means are then used to condition
the estimates of missing data. The basic equation for missing data estimation in both PXPP and MAP is:

where Px is the precipitation at the station being estimated,
Pi is the precipitation at the estimator station, n is the
number of estimating stations, i is the station being used
as an estimator, Px is the mean monthly precipitation for
station x, Pi is the mean monthly precipitation for station
i, and wi,x is the station weight, computed as:

where di,x is the distance from station x to estimator i.
The use of monthly means in Equation 1 attempts to account for orographic effects in areas having significant elevation
range. In non-mountainous areas it is assumed that there is little spatial variability in long term station means. Hence,
the ratio of station monthly means drops out of Equation 1 in such cases. Other functions in PXPP include double mass
analysis and the generation of consistency corrections. In addition, PXPP also contains correlation analyses to aid in the
determination of station weights in mountainous areas.
In mountainous areas, an isohyetal analysis is needed to compute a long term mean areal precipitation value over a
watershed in order to understand the relationship between the precipitation measured at stations and that which usually
occurs over an area. The long term mean areal value is used to derive weights for stations that are used to compute not
only the historical MAP time series but also weights for stations that are used operationally but were not in the historical
data set. This procedure helps ensure that biases are not introduced between the calibration and operational systems
when different stations are used.
Isohyetal maps are available from several sources. In some rare cases, such maps may have been developed as part of
a previous study. The method outlined by Peck and Brown [1962] to create isohyetal maps can also be used using some
of the output from PXPP. Recently, monthly digital isohyetal maps for large parts of the country have been developed
by Oregon State University for the Natural Resources Conservation Service (NRCS) as part of the Precipitation-elevation Regressions on Independent Slopes Model (PRISM) project [Daly et al., 1994]. Data from PRISM are
contained in CAP.
Once an isohyetal map is obtained or derived, the map is analyzed and modified to ensure that it is appropriate for the
period of analysis and computation of the MAP time series. Water balance analyses for the watershed in question and
surrounding watersheds can also be used to validate the isohyetal map.
After any elevation zones or sub-divisions are derived, annual or seasonal mean areal precipitation values need to be
computed for each watershed or zone using the procedures described above. These means are then used in the
computation of station weights. For this computation, Equation 3 is used:

where W is the station weight, i is the station whose weight is being computed, s is the season of the year, N is the total
number of stations with weight, R is the relative station weight, A is the long term areal mean precipitation, and S is the
station long term mean precipitation.
The determination of the relative weights R is a subjective process and is based on the user's knowledge of the basin as
well as types, coverage, and directions of storms, and station intercorrelation. Typically, station weights W sum to a
value greater than one to reflect the fact that the gages tend to catch less than the basin as a whole. Both seasonal and
annual station weights can computed.
Equation 3 provides the user with a method of calibrating a basin with data from one set of precipitation stations and then
operationally forecasting with a potentially different set of stations. Because of the use of the term A derived from the
isohyetal analysis, stations that were not part of the historical network can be added to the operational network without
introducing a bias into the computations. New stations can be added to the operational network after an estimate of the
long term station mean S is derived.
After using PXPP to perform consistency checks and compute monthly means, program MAP is used with the station
weights Wi,s to compute a time series of mean areal precipitation values. Usually, a 6 hour time step is selected, although
other time steps can be specified.
The use of gridded precipitation estimates from the NEXRAD platforms presents similar challenges. Research in the
NWS and elsewhere has shown that hydrologic model parameters calibrated using rain gage data are most likely not
directly applicable for use with radar data [Johnson et al., 1999; Smith et al., 1999; Bradley and Kruger, 1998, Finnerty
et al., 1997]. As a result, re-calibration of rain-gage based model parameters should be considered for use with radar
precipitation estimates. However, the period of NEXRAD data available for calibration is not long enough for effective
calibration in most areas of the country. Also, changes in processing algorithms may have contributed to time-dependent
inconsistencies in the data, making calibration of continuous hydrologic models a difficult task. Consequently, use of
NEXRAD data for calibration and forecasting continues to be an active area of research.
5.1.5 Generation of mean areal temperature time series. Time series of temperature are primarily needed for
use with Snow-17 as well as frozen ground computations in the SAC-SMA. The main program for computing time series
of mean areal temperature is the MAT program. MAT contains procedures for computing missing data and for
computing consistency corrections. Using observed daily maximum and minimum temperatures and station weighting
schemes, MAT computes a 6-hour time series of mean areal temperatures for a watershed. An assumed diurnal variation
is used to convert the daily maximum-minimum temperatures into a 6 hour time series. Equation 4 is the general equation
for estimating missing maximum and minimum temperatures within the MAT program for both non-mountainous and
mountainous areas:

where T is the computed maximum or minimum temperature value, T is the mean value, x is the station being estimated,
i is the estimator station, n is the number of estimator stations, and w is the weight applied to each estimator, computed
as:

where dx,i is distance, Ex,i is elevation difference and Fe is the elevation weighting factor. In non-mountainous areas,
distance is the dominant factor in determining which stations are used as estimators of missing data, so a value of zero
is used for Fe in Equation 5. For the computation of time series of mean areal temperature, station weights in non-mountainous areas are automatically computed using an inverse distance scheme.
In order to compute mean areal values of temperature over a mountainous watershed or sub-area of a watershed, seasonal
variations of maximum and minimum temperature with elevation are developed on a regional basis. These temperature-elevation relationships are developed using the program TAPLOT program as shown in Figure 2. Straight line
relationships are generally fitted to the data for each month which should represent physically realistic lapse rates,
generally in the range of 0.3 to 0.8 C/100m. Temperature-elevation relationships are primarily used to extrapolate
temperatures from lower to higher elevations due to a general lack of high elevation data in most basins.
The computation of time series of MAT in mountainous areas centers around the use of a synthetic station established
at the mean elevation of each watershed or zone. A synthetic station is one with no observed data. All data for the
station is estimated from surrounding real stations. and the synthetic station is assigned a predetermined weight of 1.0.
Mean monthly max and min temperatures for the synthetic station are derived from the temperature-elevation plots and
are used in Equations 4 and 5 to estimate missing data for the synthetic station. Using this method, an MAT time series
is derived that reflects the average conditions within each elevation zone.
As with precipitation, procedures are used to minimize biases between the calibration and operational station networks.
The same synthetic stations and corresponding mean monthly temperatures must be defined in the operational system
and given full weight. New stations can be added to the operational network after computing a best estimate of the long
term mean monthly maximum and minimum temperatures.
5.1.6 Generation of evapotranspiration data. The SAC-SMA requires evapotranspiration demand (ET
Demand) as input. ET Demand is the evaporation that occurs given that moisture is not limiting and considering both
the type and activity of vegetation. Thus, while PE is defined for an actively growing grass surface, ET Demand is based
on the actual vegetation in the area and how active that vegetation is given the time of the year and other factors. As
shown in Figure 2, two methods for generating estimates of ET Demand for calibration and operational forecasting are
available. In the first method, the SAC-SMA will accept a daily PE value in conjunction with a seasonal adjustment
curve. The second method uses mean monthly values of PE and a seasonal adjustment curve.
In the first approach, daily estimates of potential evaporation demand are computed using meteorological data from
synoptic stations and the Penman [1948] equation. In this case, the net radiation is estimated from sky cover data
according to the method of Thompson [1976]. In these cases, time series of mean areal estimates of potential evaporation
are computed using the MAPE program using a simple distance weighting scheme or user defined station weights.
However, skycover measurements at some stations have recently been discontinued so that reliable values of daily PE
can no longer be computed. In light of this, research is underway in HL to investigate new methods of computing PE.
One requirement for a new method is that any data used for calibration must have the same statistical properties as the
data used for operational forecasting.
In the second method, monthly estimates of PE are developed from published tables of evaporation pan measurements
and other information [Farnsworth and Thompson, 1982]. Average monthly pan evaporation values from stations in
and around the basin are used to derive an average monthly curve. The pan coefficient is applied to create an evaporation
demand curve. Finally, the curve is adjusted to show the average effects of transpiration, resulting in an ET Demand
curve. Traditionally, vegetative effects were estimated based on a users knowledge of the type of vegetation in the basin.
Recently, a methodology to derive these monthly adjustment factors based on Normalized Difference Vegetative Index
(NDVI) greenness fraction data has been developed in HL. This procedure has been incorporated into CAP.
In non-mountainous areas, estimates of PE are adjusted to the evaporation maps derived by Farnsworth and Peck [1982].
In mountainous areas, these maps aren't of sufficient detail to determine PE for individual watersheds or sub-watersheds.
In these areas, the recommended approach is to derive a basin-wide relationship between PE and elevation. Water
balance computations are then performed and the MAP time series is adjusted to achieve a correct water balance.
With either method of computing evapotranspiration, procedures are designed to ensure that the long term mean areal
value of potential evapotranspiration used in calibration is the same used in operational forecasting. This is accomplished
by using the free water surface evaporation maps published in Farnsworth and Peck [1982] as a standard.
5.2 Hydrologic Model Calibration
The next major step is to use the MAP and MAT time series and PE estimates as observed forcings to calibrate the
hydrologic model parameters. Primarily, manual techniques are used and a systematic and proven strategy is followed
for calibrating each of the parameters within the SAC-SMA and SNOW-17 models [Anderson, 2002; Hydrologic
Research Center, 1999]. While at times intensive, manual calibration provides the user with an opportunity to learn the
inner workings of the hydrologic models. Consequently, the user will be better equipped to use the models in an
operational setting.
The primary program used for model calibration is the Manual Calibration Program (MCP). MCP is basically the same
as the OFS with the main exception being that the hydrologic models are executed over multi-year calibration periods
rather than multi-day or multi-week forecast periods. MCP allows for the computation of a number of goodness-of-fit
statistics. A significant enhancement to the manual calibration process has been the recent development of the Interactive
Calibration Program (ICP). This tool is a powerful graphical user interface for executing MCP. ICP displays the
simulated and observed hydrographs for the run as well as the SAC-SMA and Snow-17 model states and runoff
components for the entire run period. Plate 1 shows the main displays within ICP. In this display, the hydrograph from
February 1, 1979 to April 28, 1979 is presented, along with the corresponding SAC-SMA runoff components and states
in the various SAC-SMA storages. In the extreme upper pane is displayed the rainfall hyetograph with the computed
runoff. Below that, the 6 runoff components from the SAC-SMA are displayed as a percentage, allowing the user to
clearly see which components comprise a streamflow response at any time. Below that is a pane that shows the states
of the tension and free water storages in the SAC-SMA. Lastly, the bottom pane shows the computed and observed
hydrographs. A similar display is available for the Snow-17 model.
ICP has the capability to display previous simulations so that the effects of an individual parameter change can be easily
identified. With ICP, parameter changes and subsequent model runs and output displays can be performed in seconds.
In spite of this high turnaround speed, it is advised that the user pause before displaying the new simulation and ask
himself: "What effect should I see with this change?" If the expected result is not achieved, the user is encouraged to
investigate potential causes rather than quickly making another parameter change. In this way, the process of manual
calibration produces a set of optimum parameters and gives the user more expertise with the inner workings of the
models.
Along with visual inspection fo the hydrographs, goodness-of-fit statistics are computed to guide the process as well as
to determine when the calibration phase is completed. While a large number of statistics are computed, the dominant
statistics are overall, seasonal, and flow interval biases. Also, the accumulation of the differences between simulated
and observed flows over time should be examined. A check of the statistics as well as visual evaluation of the simulated
hydrographs are performed after parameter changes to help guide the user through the process. A variety of statistical
measures are available for evaluating the final results, but these are not usually helpful when making individual parameter
changes.
Before parameter calibration begins, calibration and verification periods need to be selected. Experience has shown
that the SAC-SMA needs at least an 8 year period for parameter calibration in wet areas. In drier regions, a longer period
may be necessary in order to obtain enough events to consistently force all the model components. If possible, a
calibration period is identified that contains a number of large precipitation events as well as several extended periods
where base flow is dominant. Such a period is necessary to ensure that all the SAC-SMA components are activated a
number of times. For verification, an independent period containing flows outside of the range in the calibration period
is selected. Such a period allows the user to understand how the model might behave in an operational setting with
extreme events.
A suggested strategy for calibrating watersheds within a basin has been developed by Anderson [2002]. Generally, the
watershed with the best data and fewest complications is calibrated first. Next, other headwater areas with minimal
complications, as well as downstream local areas where a good local hydrograph can be generated, are calibrated. These
calibrations use the spatial assessment information to determine which previously calibrated parameters should be used
as initial values. Here, only parameters that need to be changed are adjusted. Lastly, parameters are assigned to
remaining watersheds from a calibrated area with similar hydrologic conditions. Minor adjustments to parameters are
sometimes possible to remove biases, but a full calibration is not possible for these basins.
Anderson's [2002] proposed strategy should not only result in realistic and spatially consistent parameters, but should
also greatly reduce the amount of time required for calibration. After the initial headwater calibrations, subsequent
calibrations should require less effort because the process is generally one of making adjustments to only a few
parameters and not performing a full calibration.
Initial values for some of the SAC-SMA model parameters can be derived through analysis of the observed streamflow
data [Anderson, 2002; Burnash, 1995; Peck, 1976]. Typically, good initial values of the base flow withdrawal
coefficients can be reliably obtained through hydrograph analysis, as can the size of the upper zone tension water storage.
In some cases, initial values of the sizes of the lower zone baseflow storages can be obtained. Alternatively, initial SAC-SMA parameters derived using the method discussed in Koren et al., [this volume] can be used. (The interested reader
is referred to Koren et al., [2000] for more details, while the work of Duan et al., [2001] discusses an application of
these initial parameters). The NWS also provides guidelines for selecting initial parameter values for the snow model
based on forest cover, typical amount of snow experienced, and other information.
Once initial values of the SAC-SMA and SNOW-17 models are obtained for the first headwater area, manual calibration
with ICP proceeds according to a systematic strategy developed by Anderson [2002]. Without a systematic procedure
and knowledge of the model, parameters could be derived that are out of a reasonable range yet still provide acceptable
statistics [Burnash, 1995]. Examples of the effects of changing each of the SAC-SMA and Snow-17 model parameters
have been developed to help the user understand how the hydrographs change [Hydrologic Research Center, 1999].
The main steps in this strategy are summarized as follows:
1. Remove gross overall errors, usually volume errors. The annual percent bias statistic should be within ±10
percent before continuing ( ± 20 percent in areas with small amounts of annual runoff). Large volume errors
are usually caused by initial parameter values way out of range, or large errors in the MAP, MAT or MAPE
time series. Errors such as these should be corrected because they will mask the effect of any subsequent
parameter changes and will hinder the calibration process.
2. Obtain reasonable simulation of observed baseflow. Even though the models will be used primarily for flood
forecasting, the best calibration results are obtained when the entire model is calibrated properly, starting with
baseflow. Since the volume of storm runoff is linked to the percolation of water to the lower zone in the SAC-SMA, the proper simulation of baseflow will result in an improved simulation of fast response storm runoff.
The size of the two baseflow storages are adjusted as well as the withdrawal coefficients. At this point it is
advisable to check for the existence of riparian vegetation effects. Important considerations here are the proper
division between fast and slower baseflow responses.
3. Adjust major snow model parameters. Here, parameters governing the melt rates and volume of snowmelt
runoff are examined. Also, if a significant number of events where the form of precipitation is not typed
correctly (i.e., rain vs. snow), it may be necessary to change the MAT time series so that the major events have
the correct form of precipitation. These changes are sometimes necessary due to deficiencies caused by the use
of a constant diurnal temperature variation and only daily maximum and minimum temperatures. Model
parameters cannot be adjusted to account for mistyping of events.
4. Examine SAC-SMA tension water capacities. These two storages act as thresholds to govern the timing of
runoff generation as well as the size of soil moisture deficits that can occur in response to evapotranspiration.
To determine the proper values of these parameters, one looks at the time when the deficits are greatest, and
then how the model responds when the deficits are filled.
5. Adjust parameters governing the generation of fast response or storm runoff. The proper separation between
baseflow and fast response runoff is examined under a wide range of soil moisture conditions. In addition,
parameters affecting the separation of fast response runoff into interflow and surface runoff are adjusted.
6. Final adjustments. These involve changes to the unit hydrograph, adding in riparian vegetation effects, and
adjustments to the evapotranspiration demand function.
Often the user will need to return to a previous step and refine a parameter value that was previously adjusted. Due to
the interactions of many of the SAC-SMA parameters, adjustments to one parameter to achieve a primary effect will also
result in a secondary effect that must be corrected through subsequent interactive parameter adjustment. Following the
calibration of the initial headwater area, the strategy described earlier for calibrating the remaining watersheds in the
basin is followed.
A common question regarding model calibration is 'when is the calibration finished?'. The NWS recommends several
criteria for evaluating when a calibration is finished:
1. All biases between the simulated and observed hydrographs have been removed such that only random error
remains. There should be no seasonal trends. Also, there should be no trends in peak flow estimation, as well
as trends at low and intermediate levels.
2. Each parameter properly models the intended portion of the streamflow hydrograph. In such cases, the
models should have a better chance of operationally simulating events outside the calibration period.
3. Parameter sets should have a logical spatial pattern among watersheds. Calibrated parameter sets for the
watersheds in a basin should logically follow the assessments derived by examining the spatial variation of
physiographic features and hydrologic response across a basin.
RFCs are encouraged to derive statistical criteria of their own in order to assess the quality of their calibrations to meet
program goals. The following statistical criteria are also suggested as targets:
1. Overall percent bias within ±5%
2. Random variation in monthly biases (ie, no positive or negative seasonal trends greater than ±5%, especially
during periods of high flows.)
3. Flow interval biases within ± 5%.
Certainly, there are many cases in which the calibration cannot achieve the suggested criteria. To a large degree, this
is governed by the availability and quality of the historical data [Burnash, 1995] and the variability of the meteorological
conditions. In such cases, it is recommended that potential causes for the final statistics be documented. These data are
then retained and made available during operational forecasting to assist the forecaster. Moreover, it should be expected
that some trends exist simply due to the limitations of lumped modeling and the use of an index to compute snowmelt.
HL is heavily engaged in the development of distributed models to take advantage of spatial variability of precipitation
and physiographic features. Approaches including semi-lumped (i.e., sub-basins) [Boyle et al., 2001; Smith et al., 1999]
have been developed that show improvement in hydrograph simulation is some cases. Recently, a gridded distributed
model has been developed and tested [Zhang et al., 2001]. Accompanying the continuing development of distributed
approaches and increasing availability of spatial data sets comes the corresponding problem of parameter estimation and
calibration. To a large extent, the calibration problem centers on the need to adjust the parameters in each computational
element when observed streamflow is available only at the basin outlet.
Within HL, several approaches for distributed model calibration are being evaluated. One approach scales the a-priori
estimates for each element using a ratio of the spatially averaged a-priori estimates to the calibrated lumped parameters.
6. AUTOMATIC CALIBRATION
Long standing collaboration with university research has led to a successful integration of automatic optimization
procedures into the NWS calibration system. These efforts have tried to remove the subjectivity and reduce overall time
required by manual calibration. Research by Duan et al., [1992] and Sorooshian et al., [1993] has led to the
incorporation of the shuffled complex evolution (SCE) scheme into the suite of available optimization procedures. Also,
an adaptive random search algorithm developed by Brazil [1989] has been made available. These methods optimize a
single objective function, such as the daily root mean square error (DRMS). Gupta et al., [1999] concluded that automatic
calibration methods have progressed to the point where they may be expected to perform with a level of skill approaching
that of a well-trained hydrologist. This does not mean that the skill of the hydrologist is no longer necessary, but rather
that more confidence may be placed in the use of these automatic tools to assist in the calibration process.
Automatic optimization has been used in NWS field offices in several ways. In some cases, automatic calibration is used
to fine tune a parameter set after manual calibration is complete. Other field personnel use automatic methods to evaluate
the parameters at an existing stage in the manual calibration process. Cooperative research between the NWS and the
University of Arizona has led to the development of a step-wise procedure that mimics the steps recommended for
manual calibration [Hogue et al., this volume; Hogue et al., 2000]. In the Multi-Step Automatic Calibration Scheme
(MACS) procedure, base flow parameters are first optimized by minimizing the log objective function. In step two, the
optimized base flow parameters are fixed and the parameters governing the generation of fast response runoff are
optimized using the Root Mean Square Error (RMSE) criteria. Lastly, the fast response parameters optimized in step
two are fixed and the base flow parameters are adjusted. Results with the MACs procedure have shown to be comparable
or slightly better than results from manual calibrations in certain cases [Hogue et al., this volume]. The MACS approach
also somewhat addresses the limitation of using one objective function for all parts of the hydrograph.
In spite of the advances in more efficient and powerful search algorithms, several drawbacks have limited the use of
automated methods. One of the main limitations of automatic approaches is that no one objective function to be
minimized works well with all parts of a streamflow hydrograph [Boyle et al., 2000]. Also, Burnash [1995] and Boyle
et al., [2000] stated that automatic calibration may tend to result in parameters that have conceptually invalid values.
Yet another concern is that unlike the approach developed by Anderson [2002], current automatic calibration techniques
cannot be guided to produce spatially consistent parameter sets among watersheds in a basin. To address this concern,
Koren et al. [this volume] propose a method of conditioning the parameter search space using a-priori estimates of model
parameters.
7. MODEL CALIBRATION AT THE RIVER FORECAST CENTERS
While the development of strategies and tools is critical to the efficiency of model calibration, the success of any effort
also hinges on the organizational structure within an RFC. Through the use of guidelines, teams, and peer review,
calibrations are better and more consistent across basins. As an example, the Northwest RFC (NWRFC) will be used
to illustrate how the calibration effort can be organized to meet objectives in an efficient manner and generate consistent
results.
Prior to any work, the calibration team first determines how to split the region into calibration areas. Hydrologic
similarities, basin soil characteristics, common geological attributes, and meteorological considerations are used to define
regions. Actual river locations to calibrate are determined by availability of data, user requests, and complexity of
hydrologic processes.
Specialists in data analysis then use the techniques describe earlier to create data files that are used by all calibrators.
Template files for MAP and MAT are produced for the calibrators. A TAPLOT is run to provide common temperature-elevation plots for deriving means for the MAT synthetic station. Evaporation data are summarized.
The calibration group then reviews data, basin hydrology, geological factors, and lists of perspective calibration points
in each region. A set of guidelines is prepared and distributed to each calibrator. These guidelines provide limits for
model parameters, basin splits, model selection, and criteria for determining when a calibration is complete. These
guidelines are reviewed and possibly modified during the course of the calibration process. All forecasters are then
assigned calibrations from the list of prospected sites.
The calibrator follows the procedures outlined in this paper. Upon completion of a calibration, it is submitted to a peer
review group for acceptance. The calibrator can sit in these reviews and often benefits from the experience and dialog
presented during these meetings. The review group is made up of 2 to 3 of the most experienced calibrators. Experience
has shown that the review process has ensured consistency and hydrologically sound calibrations.
The final step in the process is to transfer the calibration into operations. Considerable knowledge has been gained during
the one to two week period the calibrator has spent calibrating. It is during this phase, parameter sensitivities and specific
or unique hydrologic processes are discussed. The calibrator and the review team provide new forecast point training
before a point is placed into operations.
8. ILLUSTRATION OF THE CALIBRATION PROCESS
As an illustration, the procedures outlined in this paper were applied to the Oostanaula River above the USGS gage in
Rome, Georgia, and used to develop an NWS calibration training video [Hydrologic Research Center, 1999]. Figure
3 shows that the watershed contains several headwater and local basins. The letters indicate the sequence in which the
basins are calibrated. The watersed boundaries define the areas draining to RFC forecast points. While the USGS
maintains streamflow gages at points 1 and 2 in Figure 3, these points are not currently forecasted by the RFC and thus
are not explicitly modeled.

Observed streamflow data from the basins were normalized and plotted to note similarities in response amongst the
watersheds. Historical data analysis was performed for the basin as a whole, rather than as separate steps for each
watershed. A network of 31 daily and 11 hourly raingages was used in the analysis of precipitation. An MAT time series
was not developed as snow is not hydrologically important in this region. Given the spatial variability of long term
precipitation station means, a mountainous area analysis was performed. An isohyetal map was derived using the method
of Peck [1962] and subsequently integrated to derive the long term mean areal precipitation value A in Equation 3 for
each watershed. Using Equation 3, precipitation station weights were derived for each of the watersheds and 6-hour
MAP time series were developed. USGS mean daily flow data were retrieved for the calibration process.
Following the strategy proposed by Anderson [2002], the Coosawatte River above the USGS gage near Ellijay, Ga. was
selected as the watershed to calibrate first, as it had the best data and fewest complications. Initial values of the SAC-SMA were derived from analysis of the observed hydrographs and appear in Table 1.
As discussed earlier, Step 1 in the calibration process is to remove large errors in the simulation which might mask
needed parameter changes. Examining the hydrograph plots in ICP revealed that the model greatly over-simulated the
high flows and underestimated the low flows. This indicated that too much surface runoff was being generated and too
frequently. Thus, the UZFWM parameter was changed from 40mm to 80mm. After running the model with this parameter
change, the ICP display revealed that the amount of surface runoff was indeed reduced. Seasonal bias statistics for this
simulation appear in column 1 of Table 2. These results indicate a rather large bias in November, December and January.
To reduce this bias, changes were made in the ET Demand curve. The resulting statistics shown in column 2 of Table
2 indicate that the bias was reduced by this change.
Step 2 of the calibration process is to adjust the base flow parameters. Visual examination of the hydrographs at this
point in the process revealed that too much primary baseflow and not enough supplemental baseflow was being
generated. To correct these tendencies, the primary baseflow storage was decreased from 600mm to 480mm, and the
supplemental baseflow storage was increased from 125mm to 250mm. The PFREE parameter was changed from 0.1 to
0.4 to increase the amount of baseflow recharge, and the value of LZSK was reduced from 0.04 to 0.02 to slow down
the withdrawal of supplemental baseflow. After these parameter changes were made, the model was re-run and the bias
statistics in column 3 of Table 2 were generated. These results and a visual examination of the simulation in ICP revealed
a closer agreement of the simulated and observed hydrographs.
Step 3 in the process is to examine the size of the upper and lower tension water storages. As before, visual examination
of the hydrograph plots and storage components in the ICP displays revealed the needed changes. The size of the upper
zone tension water storage, UZTWM, seemed appropriate, but the size of the lower zone storage, LZTWM, needed to
be increased from 150 to 250mm. After making this change, the ICP plots revealed that the lower zone was filling up
at the appropriate time in the fall and that base flow recharge during the winter was being modeled appropriately.
Column 4 of Table 2 shows the seasonal bias statistics at this point in the calibration process.
The fourth step in the calibration strategy is to examine the division of fast and slow response portions of the
hydrographs. Primarily, this involves an analysis of the parameters controlling the percolation function, or the potential
rate at which water moves from the upper zones to the lower zones. The flow interval bias figures in column 1 of Table
3 indicate that at this point in the process, the model was overpredicting low flows and underpredicting the larger events.
To mitigate these effects, the percolation parameters were changed to reduce percolation during the wetter periods and
increase percolation during the drier periods. Also during this step, the size of the variable impervious area was changed
from 0 to 5% of the total basin area to increase peak flows during intermediate rainfall events. After making these
changes, the flow interval bias statistics in column 2 of Table 3 indicate that while the model still over predicts the low
flows, the simulation of intermediate and large events was more appropriate. Visual analysis of the simulation also
showed a better division of fast and slow runoff. Column 5 in Table 2 indicates an improvement in the overall bias
statistic.
To finish the calibration of the Coosawattee River headwater basin, final adjustments are made to reduce seasonal and
overall biases. Column 5 of Table 2 shows that at this point in the calibration process, large positive biases existed in
the winter with large negative biases occurring in the early summer. The ET-Demand curve was adjusted to increase
evapotranspiration demand in the fall, winter, and spring while reducing this demand in April, May, and June. The final
seasonal bias statistics in column 6 reveal reasonable monthly biases with a very good overall bias.
Table 4 presents final values of the bias and correlation coefficient for the calibration and verification periods for the
Coosawattee River. These statistics quantify the goodness of fit that was also apparent in a visual examination of the
simulated and observed hydrographs.
Following the sequence in Figure 3, the calibrated Ellijay parameters were used as starting values for the calibration of
Talking Rock Creek at Hinton, Ga.. In this calibration, only the parameters that needed adjustment were changed to
produce an acceptable fit. Column 1 of Table 5 shows the flow interval bias statistics that resulted by using the Ellijay
parameters as initial values for the Hinton basin. As expected from the analysis of the normalized observed flows, these
results indicate that the Ellijay parameters oversimulated the lower flows and under-estimate the high flow events for
the Hinton basin. As a first step to correcting these biases, the percolation curve was lowered to generate more fast
response runoff. The LZFSM parameter was changed from 400mm to 285mm while the LZFPM parameter was adjusted
from 480mm to 340mm. Both a visual examination of the computed and observed hydrographs and the results in Column
2 of Table 5 indicate these changes to the percolation curve produced a better fit. After these percolation changes, visual
examination of the computed and observed hydrographs for the Hinton basin showed that more surface runoff needed
to be generated. To achieve this, the size of the upper zone free water storage (UZFWM) was reduced from 80mm to
55mm. The resulting flow interval bias statistics are shown in column 3 of Table 5 and show improvement in the bias
figures for large events with a corresponding degradation in the bias statistics for medium flow levels. A visual
examination of the hydrographs also confirmed the use of a smaller value of UZFWM for large events.
To complete the calibration of the Hinton basin, the value of upper zone free water withdrawal coefficient, UZK, was
increased from 0.2 to 0.3 to generate a faster interflow response. Also, the RIVA parameter was increased to model the
effects of riparian vegetation evaptranspiration in the dry summer months. In addition, the amount of constant
impervious area was reduced so that the model did not respond as much to every rainfall event. Column 4 of Table 5
presents the final flow interval bias statistics after these last parameter changes were made.
Calibration of the entire watershed continues according to the sequence shown in Figure 3. In this step, the final Hinton
parameters are used as the initial parameters for the Conasauga River at the USGS gage in Tilton, Ga.. As before, only
the parameters which need to be changed are adjusted. For this watershed, the analysis of the simulated and observed
hydrographs revealed that more fast response runoff was needed. The statistics for the initial run in Table 6 also show
that the base flows were greatly overpredicted and the larger events were underpredicted.
To generate more fast response runoff, the percolation function was reduced to 40% of its initial value by reducing the
LZFSM parameter from 285mm to 115mm and the LZFPM parameter from 340mm to 135mm Also during this step, the
value of UZK was increased from 0.3 to 0.4 to speed up the generation of interflow. After these changes, the subsequent
simulation improved both visually and statistically. However, the hydrographs showed that subsequent changes to the
supplemental base flow needed to be made. These included changing the LZSK parameter from 0.02 to 0.03 and
increasing the size of the supplemental base flow storage, LZFSM, from 115mm back to 135mm. As seen in column
2 of Table 6, the flow interval bias statistics for the second trial have been reduced across all flow ranges. The
corresponding seasonal bias statistics for this simulation are shown in column 1 of Table 7.
Visual examination of the hydrographs after these changes revealed that the summer events were being overpredicted,
indicating that the size of the upper zone tension water storage parameter UZTWM need to be increased from 100mm
to 150mm. In addition, the ET-Demand curve was adjusted to reduce the seasonal bias shown in column 1 of Table 7.
After these changes were made, improved seasonal bias statistics resulted and are shown in column 2 of Table 7. Visual
inspection of the simulations also showed improvement from these changes. However, as seen in column 2 of Table 7,
a large bias still remained for the summer months. The shape of the simulated and observed hydrographs during this
period indicated that riparian vegetation evapotranspiration effects were present. To model these effects, the value of
the RIVA parameter was increased from 0.0 to 0.05, indicating that 5% of the basin area was affected by riparian
vegetation.
After making the change to the RIVA parameter, the model was re-run and the flow interval statistics in column 3 of
Table 6 were generated. The corresponding seasonal bias statistics for this simulation are shown in column 3 of Table
7. These results show acceptable levels of bias. Along with a visual examination of the simulation, these statistics
showed that the calibration of the Tilton basin was complete.
Following the calibration sequence shown in Figure 3, the local area above the USGS gage in Rome, Ga. was calibrated.
In Figure 3, this is the area between points 8 and 9. To begin this calibration, the calibrated parameters from the most
hydrologically similar basin were used as initial values. The Tilton parameters were used as this basin was most similar
to the Rome local area. To define the local area hydrograph, the unit hydrograph from Tilton was used but scaled to
reflect the drainage area of the Rome local area. The channel routing parameters were obtained from the RFC operational
files. The steps involved in calibrating this local area were also applied to the calibration of the local area between points
6 and 7 in Figure 3.
After minor modification to the channel routing parameters, it was clear that the Tilton SAC-SMA parameters worked
quite well in the simulation of the Rome local area. Only a decrease in the RIVA parameter from 0.05 to 0.0 was
required as the Rome local area showed no evidence of evapotranspiration from riparian vegetation. The final flow
interval bias statistics in Table 8 and the final seasonal bias statistics in Table 9 show the adjustment to the RIVA
parameter resulted in good statistics. The large bias in the lowest flow interval of Table 8 reflects the noise in the derived
local area observed hydrograph. The local area at Rome, Ga. represents only about 25% of the total drainage area above
this point.
As stated earlier, the final step in the calibration of a watershed is to assign calibrated parameters to remaining areas.
These final areas are usually local areas that are too small compared to the total drainage area to generate a reasonable
local area observed hydrograph against which to calibrate. The regions labeled D in Figure 3 were treated in this manner.
Table 10 presents the parameters that resulted from the calibration of the Oostanaula watershed. It can be seen that after
the initial calibration of the Ellijay basin, only a few parameters were adjusted in the subsequent calibration of
neighboring basins.
This example shows the efficiency of the regional approach to calibration in that only the Ellijay watershed required a
significant amount of manual calibration effort. Far less time was required to calibrate the other watersheds due to the
use of calibrated parameters as starting points for hydrologically similar watersheds. Equally important is the fact that
the final calibrated parameters exhibit a spatial pattern that is quite reasonable considering the spatial variation in
physiographic features as well as the comparison of observed streamflow hydrographs.
Table 11 presents two of the summary statistics for the entire period of record. It can be seen that in all basins, the bias
statistic is well within the recommended target criteria. Good values of the correlation coefficient were also obtained.
9. SUMMARY
The National Weather Service has continued to develop a comprehensive set of procedures and tools to facilitate the
calibration of hydrologic models. A logical and systematic strategy has been developed for manual calibration of the
SAC-SMA and Snow-17 models for an individual watershed. Moreover, an efficient strategy for calibrating the
additional watersheds within a river basin has been developed. This strategy leads to sets of parameters that make sense
considering the spatial variability of physiographic features amongst the watersheds in a basin. In addition, the use of
guidelines, teams, and peer reviews at RFCs has proven to generate quality calibrations in an efficient manner.
Through manual calibration, the hydrologist is able to learn the inner workings of the model and understand the
sensitivities to different forcings and model parameters. In this way, the hydrologist is better prepared for the forecasting
environment in which unusual conditions may be encountered. A thorough understanding of the model function is
important when a user is making short term and long term forecasts.
10. RECOMMENDATIONS
While a number of tools and recommended procedures have been developed and fielded in the NWS, numerous
enhancements to the existing programs should be made. Past efforts such as the development of ICP and IDMA have
proven that significant reductions can be realized in the amount of time required for calibration. Additional
enhancements are critical considering the national scope of the model calibration and implementation efforts in the NWS.
Perhaps what is most needed is a re-design of the Calibration System so that the functions of the MAP, MAT, MAPE,
PXPP, TAPLOT, MCP/ICP, CAP and other programs are retained but more efficiently linked, perhaps under the
umbrella of one parent tool. Such a re-design would incorporate the latest data handling and display techniques.
Currently, the programs mentioned exist as stand-alone entities, requiring a good bit of data manipulation on the part of
the user. Also, some of the functional redundancy could be eliminated. For example, each of the MAP, MAT, MAPE,
and PXPP programs contains a double mass analysis capability. A re-designed Calibration System might need to have
only one such capability.
In addition to software enhancements, continued research in several areas is also needed. Research related to automatic
optimization is necessary, especially in the development of multi-objective calibration strategies. More objective methods
could be developed for deriving station weights in mountainous areas, as well as determining the need to make
consistency corrections to station data. In addition, refined methods of computing estimates of evapotranspiration are
needed. The use of instantaneous temperatures to compute an MAT time series for calibration would greatly reduce the
errors resulting from the use of a fixed diurnal variation in conjunction with daily maximum and minimum temperature
values.
Acknowledgements. The authors are indebted to Dr. Eric Anderson, formerly of the Hydrology Lab, for developing much
of the information regarding calibration of the NWS snow and rainfall-runoff models during his long and productive
career with the NWS. Dr. Anderson is currently a consultant to the NWS Hydrology Lab.
APPENDIX:
CURRENT CAPABILITIES AND DATA SETS AVAILABLE IN THE CALIBRATION ASSISTANCE PROGRAM (CAP)
1. CAPABILITIES
The CAP is an Arc/View application. Its capabilities include the following.
1. Derive area-elevation curves
2. Sub-divide basins based on elevation zones
3. Derive elevation-precipitation plots
4. Display defined zones on top of other data layers (e.g. precipitation, elevation)
5. Compute basin mean, max, and min values of: (may also compute for each elevation zone defined within a
basin)
5.1 precipitation (monthly, annual, and seasonal)
5.2 potential evaporation (monthly, annual, and seasonal)
5.3 potential evaporation adjustment factors
5.4 percent forest
5.5 percent of each forest type
5.6 soil-based estimates for 11 SAC-SMA parameters
6. Display selected NOHRSC historical snow images from (1990-1995)
2. DATA SETS
1. Digital Elevation Model (DEM) 4km resolution
2. Percent of forest cover on 1km grid
3. Forest type on 1km grid
4. PRISM annual and monthly precipitation grids.
5. Annual and monthly potential evaporation grids
6. Soil type, depth, and texture for 11 layers
7. Snow cover grids for 1990-1995
8. State boundaries
9. EPA River Reach Files (RF1)
REFERENCES
Anderson, E.A., 'Calibration of Conceptual Hydrologic Models for Use in River Forecasting', NOAA Technical Report, NWS 45,
Hydrology Laboratory, 2002, copies available upon request.
Anderson, E.A.,'A Point Energy and Mass Balance Model of a Snow Cover', NOAA Technical Report NWS 19, February, 1976,
copies available upon request.
Anderson, E.A., 'National Weather Service River Forecast System - Snow Accumulation and Ablation Model', NOAA Technical
Memorandum NWS HYDRO-17, November, 1973, copies available upon request.
Armstrong, B.B., 'Derivation of Initial Soil Moisture Accounting Parameters from Soil Properties for the National Weather Service
River Forecast System', NOAA Technical Memorandum NWS Hydro 37, 1978, copies available upon request.
Bonnin, G., 'The NOAA Hydrologic Data System', 12th International Conference on Interactive Information and Processing System
(IIPS) for Meteorology, Oceanography, and Hydrology, Atlanta, Georgia , January 28-February 2, 1996.
Boyle, D.P., H.V. Gupta, S. Sorooshian, V. Koren, Z. Zhang, and M. Smith,'Towards improved streamflow forecasts: The value
of semi-distributed modeling,' Water Resour. Res. Vol. 37, No. 11, 2749-2759, 2001.
Boyle, D.P., H.V. Gupta, and S. Sorooshian,'Toward Improved Calibration of Hydrologic Models: Combining the Strengths of
Manual and Automatic Methods', Water Resour. Res., Vol. 36, No. 12, 3663-3674, 2000.
Bradley, A.A., and A. Kruger, 'Recalibration of Hydrologic Models for use with WSR-88D Precipitation Estimates', preprints the
special Symposium on Hydrology, AMS, 302-305, 1998.
Brazil, L.E.,'Multilevel Calibration Strategy for Complex Hydrologic Simulation Models', NOAA Technical Report, NWS 42,
Hydrology Lab, Silver Spring, Md, 1989, copies available upon request.
Brazil, L.E., and M.D. Hudlow, 'Calibration Procedures Used with the National Weather Service River Forecast System', in Water
and Related Land Resource Systems, edited by Y.Y. Haimes and J. Kindler,pp 457-466, Pergamon, Tarrytown, N.Y., 1981.
Burnash, R.J.C., 'The NWS River Forecast System - Catchment Model', Chapter 10, in Computer Models of Watershed Hydrology,
Vijay P. Singh, editor, Water Resources Publications, 1995.
Burnash, R. J. C., R. L. Ferral, and R. A. McGuire, 'A generalized streamflow simulation system - Conceptual modeling for digital
computers', Technical Report, Joint Federal and State River Forecast Center, U.S. National Weather Service and California
Department of Water Resources, Sacramento, California, 204pp. 1973.
Daly, C., R.P. Neilson, and D.L. Phillips, 'A Statistical-Topographic Model for Mapping Climatological Precipitation over
Mountainous Terrain', J. Applied Meteorology, Vol. 33, No. 2, February, pp. 140-158, 1994.
Duan, Q., J. Schaake, and V. Koren, 'A Priori Estimation of Land Surface Model Parameters', In Land Surface Hydrology,
Meteorology, and Climate: Observation and Modeling, V. Lakshmi, et al. (Ed.), Water Science and Application, Vol. 3, AGU,
Washington, DC, 77-94, 2001.
Duan, Q., S. Sorooshian, and V.K. Gupta,'Effective and Efficient Global Optimization for Conceptual Rainfall-Runoff Models',
Water Resour. Res., 28(4), 1015-1031, 1992.
Farnsworth, R.K., and E.L. Peck, 'Evaporation Atlas for the Contiguous 48 United States', NOAA Technical Report NWS 33, U.S.
Department of Commerce, 1982, copies available upon request.
Farnsworth, R.K., and E.S. Thompson,'Mean Monthly, Seasonal, and Annual Pan Evaporation for the United States', NOAA
Technical Report NWS 34, U.S. Department of Commerce, 1982, copies available upon request.
Finnerty, B.D., M.B. Smith, D.J. Seo, D.J., V.I. Koren, and G.E. Moglen, 'Space-Time Scale Sensitivity of the Sacramento Model
to Radar-Gage Precipitation Inputs', J. Hydrology, 203, 21-38, 1997.
Fread, D. L., R.C. Shedd, G.F. Smith, R. Farnsworth, C.N. Hoffeditz, L.A. Wenzel, S.M. Wiele, J.A. Smith, and G.N.
Day,'Modernization in the National Weather Service River and Flood Program', Weather and Forecasting, Vol. 10, No. 3,
September, 477-484, 1995.
Gupta, H.V., S. Soorooshian, and P.O. Yapo, 'Status of Automatic Calibration for Hydrologic Models: Comparison with Multilevel
Expert Calibration', J. of Hydrologic Engineering, Vol. 4, No. 2, pp. 135-143, April, 1999.
Hogue, T., S. Sorooshian, S., H. Gupta, A. Holz, and D. Braatz, 'A Multistep Automatic Calibration Scheme for River Forecasting
Models', J. Hydrometeorology, Vol. 1, No. 6. December, pp. 524-542, 2000.
Hydrologic Research Center (HRC), Producer: "Calibration of the Sacramento Soil Moisture Accounting Model, Demonstration of
an Interactive Calibration Approach." NOAA Video Series: VHS Video (5hrs and 15min) and Companion Notebook (200 pp.).
National Oceanic and Atmospheric Administration, National Weather Service, Office of Hydrologic Development, Silver Spring,
MD, May, 1999, copies available upon request.
Johnson, D., M. Smith, V.I. Koren, and B. Finnerty, 'Comparing Mean Areal Precipitation Estimates from NEXRAD and Rain Gauge
Networks', J. Hydrologic Engineering, Vol. 4, No. 2, April, 117-124, 1999.
Koren, V.I., B.D. Finnerty, J.C. Schaake, M.B. Smith, D.J. Seo, and Q.Y. Duan,'Scale Dependencies of Hydrologic Models to Spatial
Variability of Precipitation', J. Hydrology, 217, 285-302, 1999.
Koren, V.I., M.B. Smith, D. Wang, and Z. Zhang, 'Use of Soil Property Data in the Derivation of Conceptual Rainfall-Runoff Model
Parameters', 15th Conference on Hydrology, American Meteorological Society, Long Beach California, 103-106, 2000.
Larson, L.W., R.L. Ferral, E.T. Strem, A.J. Morin, B. Armstrong, T.R. Carroll, M.D. Hudlow, L.A. Wenzel, G.L. Schaefer, and
D.E. Johnson,'Operational Responsibilities of the National Weather Service River and Flood Program', Weather and Forecasting,
Vol. 10, No. 3, September, 465-476, 1995.
Monroe, J.C., and E.A. Anderson, 'National Weather Service River Forecasting System', ASCE J. Hydraulics Division, Vol. 100,
No. HY5, pp. 621-630, 1974
Pan, J., G.M. Bonnin, R.M. Motl, and H.Friedeman, 'Recent Developments in Data Analysis Quality Control and Data Browsing
at the National Weather Service Office of Hydrology', 78th Annual AMS Meeting, Phoenix, Arizona, January, 1998.
Peck, E.L,'Catchment Modeling and Initial Parameter Estimation for the National Weather Service River Forecast System', NOAA
Technical Memorandum NWS HYDRO-31, 1976.
Peck, E.L, and M.J. Brown,'An Approach to the Development of Isohyetal Maps for Mountainous Areas', J. Geophys. Res., Volume
67, No. 2, February, 681-694, 1962.
Penman, H.L.,'Natural Evaporation from Open Water, Bare Soil, and Grass', Proceedings, Royal Society, Series A, Vol. 193, 1948.
Smith, M.B., V.I. Koren, B.D. Finnerty, and D. Johnson, 'Distributed Modeling: Phase 1 Results', NOAA Technical Report NWS
44, February, 1999. Copies available upon request.
Sorooshian, S., Q. Duan, and V.K. Gupta, 'Calibration of Rainfall-Runoff Models: Application of Global Optimization to the
Sacramento Soil Moisture Accounting Model', Water Resour. Res. 29(4), pp. 1185-1194, 1993.
Stallings, E.A., and L.A. Wenzel, 'Organization of the River and Flood Program in the National Weather Service', Weather and
Forecasting, Vol. 10, No. 3, September, 457-464, 1995.
Thompson, E.S., 'Computation of Solar Radiation from Sky Cover', Water Resour. Res., Vol. 12, No. 5, pp. 859-865, 1976.
Zhang, Z., V. Koren, M. Smith, and S. Reed, 'Application of a Distributed Modeling System Using Gridded NEXRAD Data',
Proceedings, Fifth Int'l. Symposium on Hydrological Applications of Weather Radar -Radar Hydrology-, pp. 427-432, Nov. 19-22, Heian-Kaikan, Kyoto, Japan.
1Michael Smith, 1Victor Koren, 1Seann Reed, and 1Ziya Zhang, Hydrology Laboratory, Office of Hydrologic Development,
NOAA/National Weather Service, 1325 East-West Highway, Silver Spring, Maryland, 20910, USA.
2Donald Laurine, Northwest River Forecast Center, NOAA/National Weather Service, 5241 NE 122 Avenue, Portland, Oregon,
92730-1089,USA.
1Hydrology Laboratory, Office of Hydrologic Development, NOAA/National Weather Service
2Northwest River Forecast Center, NOAA/National Weather Service
Plate 1. The ICP Display of the SAC-SMA Model Showing Runoff Components, Soil Moisture Zone Contents, and
Corresponding Simulated and Observed Hydrographs.

Table 1. Initial SAC-SMA Parameter Values for the Coosawattee
River above the USGS Gage in Ellijay, Georgia.
| Parameter |
Initial Value |
| Size of Upper Zone Tension Water Storage,
mm (UZTWM) |
100.0 |
| Size of Upper Zone Free Water Storage, mm
(UZFWM) |
40.0 |
| Upper Zone Free Water Withdrawal
Coefficient (UZK) |
0.2 |
| Percent of Basin that is Impervious (PCTIM) |
0.04 |
| Percent of Basin that is Variably Impervious
(ADIMP) |
0.0 |
| Size of Lower Zone Tension Water Storage,
mm (LZTWM) |
150.0 |
| Size of Primary Baseflow Storage, mm
(LZFPM) |
600.0 |
| Size of Supplemental Baseflow Storage, mm
(LZFSM) |
125.0 |
| Primary Baseflow Withdrawal Coefficient
(LZPK) |
0.002 |
| Supplemental Baseflow Withdrawal
Coefficient (LZSK) |
0.04 |
| Percolation Function Parameter (ZPERC) |
25.0 |
| Percolation Function Parameter (REXP) |
2.0 |
Table 2. Monthly Percent Bias Statistics for the Calibration of
the Coosawattee River at Ellijay, Georgia.
Mon. |
Percent Bias |
| Trial |
| 1 |
2 |
3 |
4 |
5 |
6 |
| Oct. |
20.5 |
15.5 |
7.9 |
2.6 |
-1.1 |
-3.2 |
| Nov. |
38.5 |
27.5 |
11.4 |
8.6 |
6.2 |
-0.1 |
| Dec. |
51.4 |
36.2 |
21.1 |
17.7 |
17.0 |
10.1 |
| Jan. |
39.5 |
26.8 |
15.6 |
11.9 |
12.9 |
7.2 |
| Feb. |
27.0 |
13.5 |
12.8 |
9.4 |
11.0 |
7.4 |
| Mar. |
12.0 |
-0.6 |
-3.3 |
-5.0 |
-2.8 |
-3.2 |
| April |
-4.8 |
-11.4 |
-7.2 |
-9.3 |
-8.9 |
-6.5 |
| May |
-15.7 |
-18.5 |
-6.7 |
-9.1 |
-9.5 |
-4.9 |
| June |
-26.6 |
-28.9 |
-9.2 |
-13.0 |
-13.6 |
-8.3 |
| July |
-8.4 |
-10.8 |
1.3 |
-1.5 |
-3.0 |
1.5 |
| Aug. |
-5.0 |
-7.3 |
2.8 |
-1.3 |
-4.0 |
0.1 |
| Sept. |
9.0 |
6.4 |
10.3 |
6.15 |
2.4 |
4.6 |
| Over-all |
11.4 |
2.9 |
3.3 |
0.4 |
0.2 |
0.0 |
Table 3. Flow Interval Bias Statistics for the Calibration of the
Coosawattee River at Ellijay, Ga.
Flow Interval, cms. |
Percent Bias |
| Trial |
| 1 |
2 |
| 0.0 - 3.5 |
8.9 |
9.5 |
| 3.5 - 5.5 |
1.0 |
0.3 |
| 5.5 - 10.0 |
-1.5 |
-3.3 |
| 10.0 - 20.0 |
2.1 |
0.4 |
| 20.0 - 50.0 |
2.7 |
2.8 |
| 50.0 - 140.0 |
-7.0 |
-2.3 |
| > 140.0 |
-17.3 |
-8.3 |
Table 4. Statistics for the Calibration and Verification Periods
for the Coosawattee River at Ellijay, Ga..
Statistic |
Period |
| Calibration
WYa 75-84 |
Verification
WY 64-74 |
Verification
WY 95-93 |
| Bias (%) |
-0.6 |
3.5 |
-3.5 |
| Correlation
(daily flows) |
0.940 |
0.935 |
0.914 |
aWY denotes Water Year, i.e., October 1 to September 30.
Table 5. Flow Interval Bias Statistics for the Calibration of
Talking Rock Creek at Hinton, Ga.
Flow
Interval, cms |
Percent Bias |
|
Trial |
|
1 |
2 |
3 |
4 |
| 0.0 - 1.8 |
64.2 |
39.1 |
45.6 |
4.4 |
| 1.8 - 2.8 |
21.9 |
3.55 |
8.2 |
-8.6 |
| 2.8 - 5.0 |
16.0 |
4.05 |
7.1 |
-4.9 |
| 5.0 - 10.0 |
7.2 |
5.91 |
5.0 |
-2.35 |
| 10.0 - 25.00 |
-4.6 |
11.0 |
4.4 |
6.7 |
| 25.00 - 75.00 |
-23.7 |
-10.5 |
-15.2 |
-7.2 |
| >75.00 |
-46.1 |
-30.8 |
-4.0 |
-5.9 |
1 - Initial run using Ellijay Parameters
Table 6. Flow Interval Bias Statistics for the Calibration of the
Conasauga River at Tilton, Ga.
Flow Interval, cms. |
Percent Bias |
| Trial |
| 1 |
2 |
3 |
| 0.0 - 5.0 |
180.8 |
23.7 |
3.1 |
| 5.0 - 15.0 |
88.5 |
3.2 |
-4.1 |
| 15.0 - 50.0 |
19.5 |
1.5 |
4.0 |
| 50.0 - 100.0 |
-8.9 |
9.0 |
8.3 |
| 100.0 - 200.0 |
-27.4 |
-2.2 |
-2.2 |
| 200.0 - 400.0 |
-33.7 |
-1.9 |
-2.7 |
| >400.0 |
-34.2 |
-5.5 |
-5.7 |
1 - Initial run using Hinton Parameters
Table 7. Seasonal Bias Statistics for the Conasauga River at
Tilton, Ga.
| Month |
Percent Bias |
| Trial |
| 1 |
2 |
3 |
| Oct. |
29.5 |
10.8 |
7.3 |
| Nov. |
7.25 |
0.5 |
-0.3 |
| Dec. |
1.0 |
1.5 |
1.4 |
| Jan. |
-0.6 |
4.9 |
4.9 |
| Feb. |
-7.4 |
-0.5 |
-0.6 |
| Mar. |
-6.5 |
-0.2 |
-0.3 |
| April |
-3.4 |
1.9 |
1.8 |
| May |
4.5 |
3.6 |
2.6 |
| June |
8.8 |
4.3 |
1.0 |
| July |
11.6 |
-2.8 |
-7.6 |
| Aug. |
21.2 |
-0.2 |
-7.9 |
| Sept. |
43.6 |
14.3 |
-7.8 |
| Overall |
1.7 |
2.2 |
1.9 |
Table 8. Final Flow Interval Bias Statistics for the Calibration of
the Local Area above Rome, Ga.
| Flow Interval, cms. |
Final Percent Bias |
| 0.0 - 1.0 |
4712.1 |
| 1.0 - 10.0 |
20.3 |
| 10.0 - 20.0 |
-3.2 |
| 20.0 - 75.0 |
-5.14 |
| 75.0 - 150.0 |
-10.0 |
| 150.0 - 300.0 |
-13.9 |
| >300.0 |
-2.0 |
Table 9. Seasonal Bias Statistics for the Calibration of the Local
Area above Rome, Ga..
| Month |
Percent Bias |
| Oct. |
2.3 |
| Nov. |
2.6 |
| Dec. |
-1.0 |
| Jan. |
-4.4 |
| Feb. |
-7.6 |
| Mar. |
-5.6 |
| April |
-2.2 |
| May |
8.14 |
| June |
13.4 |
| July |
2.6 |
| Aug. |
-4.6 |
| Sept. |
4.2 |
| Overall |
-2.0 |
Table 10. Parameter Summary for the Calibration of the Oostanaula
River Basin.
Parameter |
Ellijay
Initial
Value |
Ellijay
Final
Value |
Hinton
Final |
Tilton
Final |
Rome
Local
Area |
| UZTWM, mm |
100.0 |
100.0 |
100.0 |
150.0 |
150.0 |
| UZFWM, mm |
40.0 |
80.0 |
55.0 |
55.0 |
55.0 |
| UZK |
0.2 |
0.2 |
0.3 |
0.4 |
0.4 |
| PCTIM |
0.04 |
0.04 |
0.02 |
0.02 |
0.02 |
| ADIMP |
0.0 |
0.05 |
0.05 |
0.05 |
0.05 |
| LZTW, mm |
150.0 |
250.0 |
250.0 |
150.0 |
150.0 |
| LZFPM, mm |
600.0 |
480.0 |
340.0 |
135.0 |
135.0 |
| LZFSM, mm |
125.0 |
400.0 |
285.0 |
135.0 |
135.0 |
| LZPK |
0.002 |
0.002 |
0.002 |
0.002 |
0.002 |
| LZSK |
0.04 |
0.02 |
0.02 |
0.03 |
0.03 |
| ZPERC |
25.0 |
80.0 |
80.0 |
80.0 |
80.0 |
| REXP |
2.0 |
3.0 |
3.0 |
3.0 |
3.0 |
| PFREE |
0.1 |
0.4 |
0.4 |
0.4 |
0.4 |
Table 11. Statistical Summary of the Calibration of the Oostanaula
River Basin: Percent Bias and Correlation Coefficient R.
Statistic |
Watershed and Period |
| Ellijay
WY
64-93 |
Hinton
WY
75-93 |
Tilton
WY
49-93 |
Rome
WY
49-93 |
| Bias (%) |
-0.2 |
-1.5 |
-1.1 |
-0.1 |
| R (daily flows) |
0.928 |
0.941 |
0.951 |
0.988 |








